Fundamentals Of Computer Graphics 第二章 数学基础

这一章打了很多基础的数学铺垫，还是只把感兴趣的记下来吧。

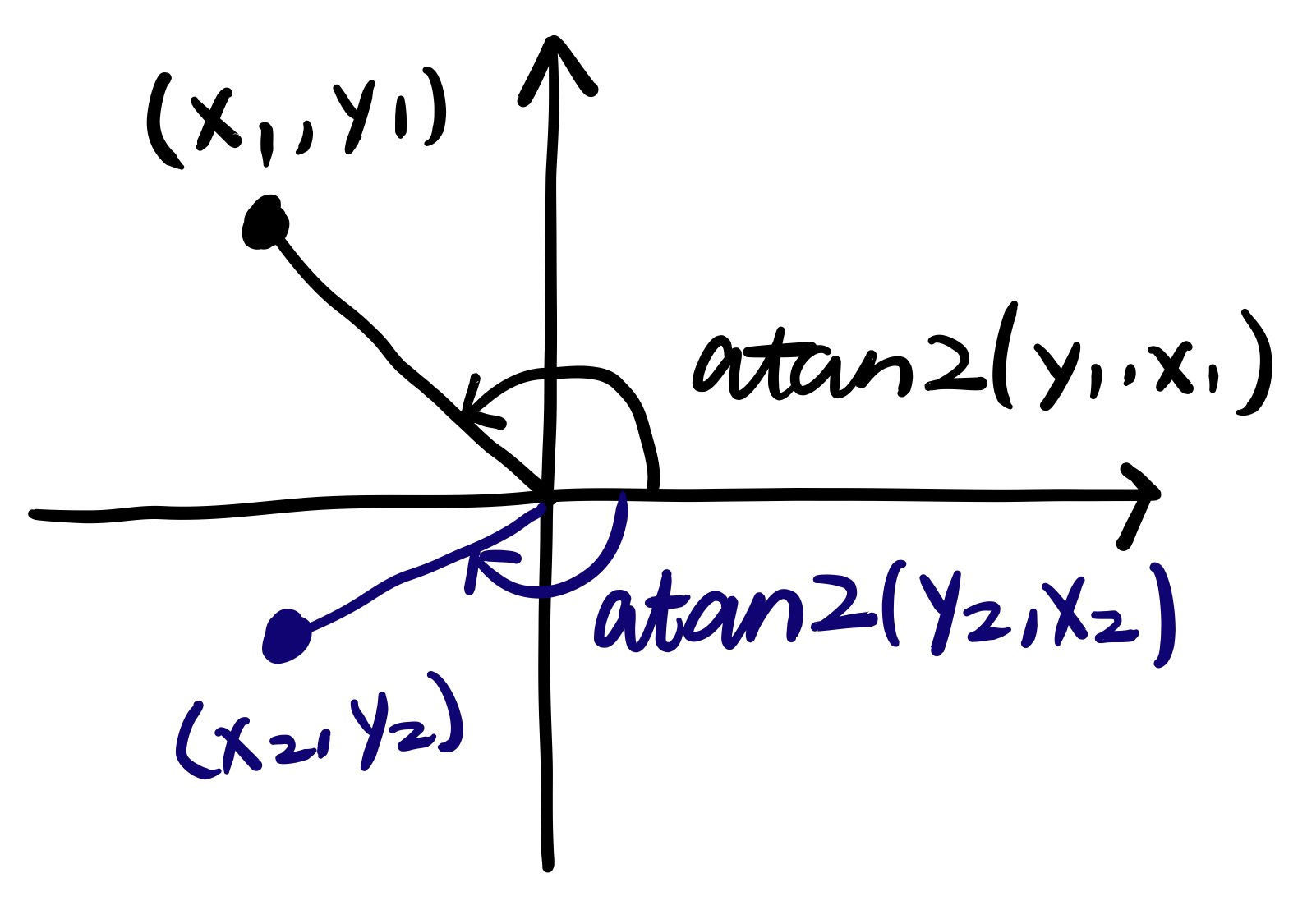
$\mathrm{atan2}(y,x)$：和普通的反正切类似，但是因为输入的是2D坐标，所以输出范围变成了$(-\pi,\pi]$。

平面三角形的一些理论

表示方法

要表示一个三角形，最trivial的方法是存储它的三个顶点坐标$\mathbf a$、$\mathbf b$和$\mathbf c$。在平面中，我们可以用叉乘的$z$坐标计算三角形的面积

$$S=\frac{1}{2}\left|\begin{matrix}x_b-x_a&y_b-y_a\\x_c-x_a&y_c-y_a\end{matrix}\right|,$$

当$\mathbf a$、$\mathbf b$和$\mathbf c$代表的顶点按逆时针顺序排序时，$S$为正，顺时针则为负。

一般来说，几何体的信息是保存到三角形的顶点里的，而在渲染三角形内部时我们使用插值方法获取数据。

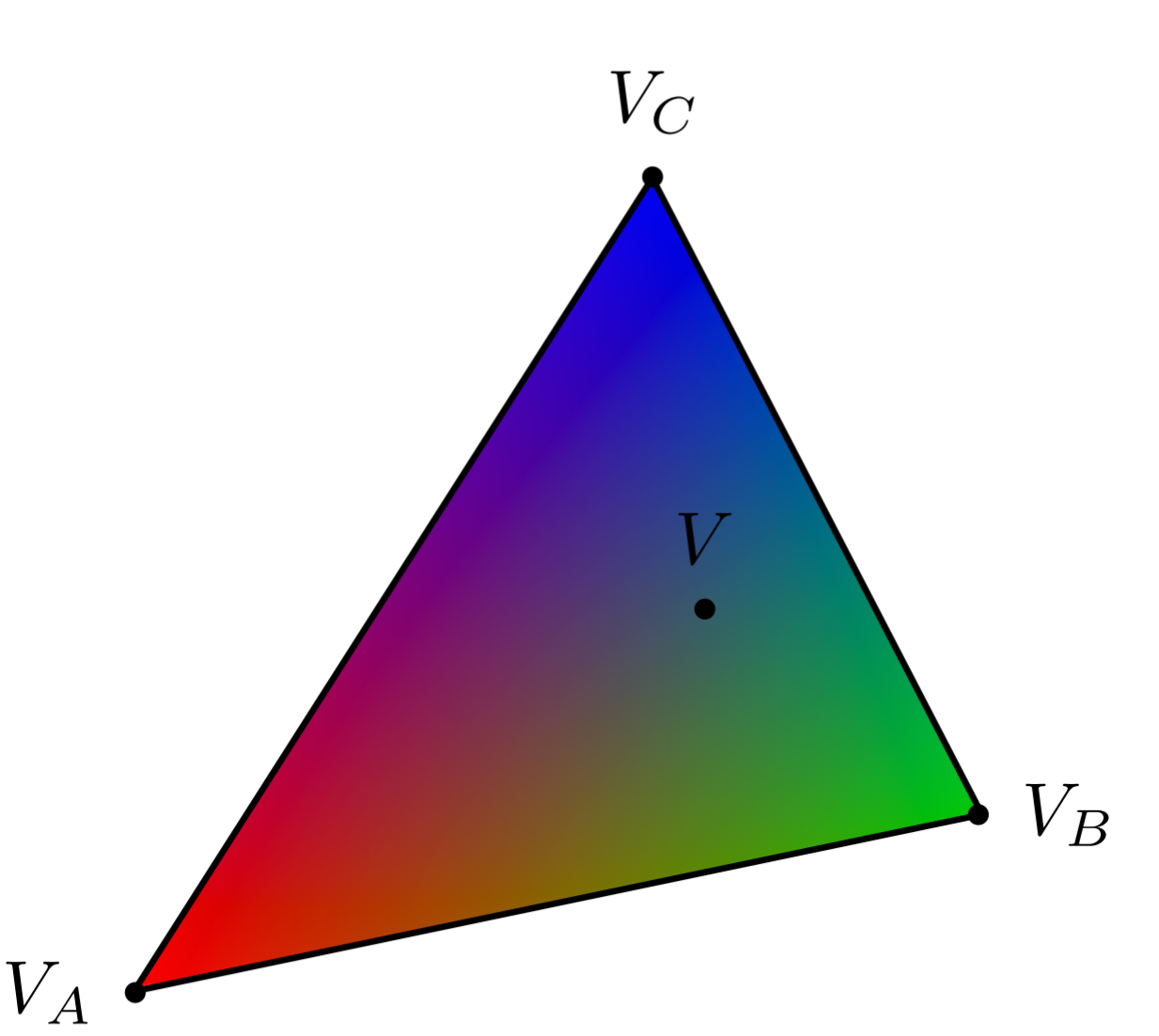
为了在三角形中方便地进行插值，我们以两边为轴，其相交的顶点为原点建立重心坐标系。

重心坐标系

在三角形$\Delta ABC$中，以$A$为原点，$\vec{AB}$、$\vec{AC}$为基向量建成的坐标系称作重心坐标系。

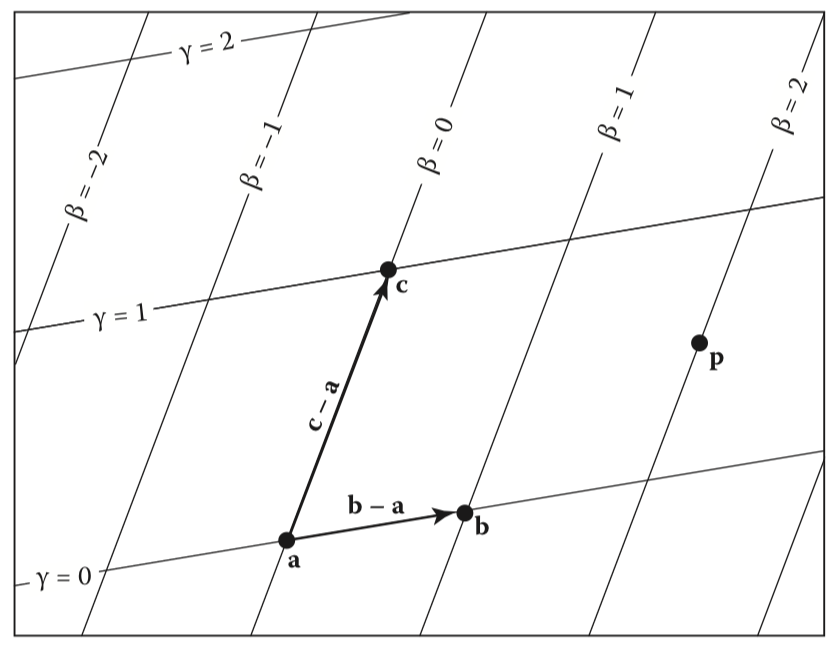
设点在坐标系中的坐标是$(\beta,\gamma)$，那么它的位置矢量$\mathbf p=\mathbf a+\beta(\mathbf b-\mathbf a)+\gamma(\mathbf c-\mathbf a)$，或者记为$\mathbf p=(1-\beta-\gamma)\mathbf a+\beta b+\gamma\mathbf c$，通常我们会令$\alpha=1-\beta-\gamma$采用对，从而得到对称记法

$$\begin{equation} \mathbf p=\alpha\mathbf a+\beta\mathbf b+\gamma\mathbf c. \end{equation}$$

当且仅当$0<\alpha,\beta,\gamma<1$时，点在三角形内部。

设$\mathbf a=(x_a,y_a)$，$\mathbf b=(x_b,y_b)$，$\mathbf c=(x_c,y_c)$，$\mathbf p=(x_p,y_p)$，则以上$\mathbf p$的表达式可以记为

$$\left( \begin{matrix} x_b-x_a&x_c-x_a\\ y_b-y_a&y_c-y_a \end{matrix} \right) \left( \begin{matrix} \beta\\\gamma \end{matrix} \right)= \left( \begin{matrix} x_p-x_a\\ y_p-y_a \end{matrix} \right)$$

通过这个方程可以解出$\beta$和$\gamma$。要求$\beta$和$\gamma$，有另一种更直观的方法，如果我们取直线$AC$的方程$f_{AC}(x,y)=0$，将点的坐标带入左侧的函数后，得到的数值与点到直线的距离成正比，直线两侧的点代入函数后得到的值符号相反。这样我们就有如下的式子：

$$\beta=\frac{f_{AC}(x_p,y_p)}{f_{AC}(x_b,y_b)}=\frac{x_p(y_c-y_a)-y_p(x_c-x_a)+y_ax_c-x_ay_c}{x_b(y_c-y_a)-y_b(x_c-x_a)+y_ax_c-x_ay_c},\\ \gamma=\frac{f_{AB}(x_p,y_p)}{f_{AB}(x_c,y_c)}=\frac{x_p(y_c-y_a)-y_p(x_c-x_a)+y_ax_b-x_ay_b}{x_c(y_b-y_a)-y_c(x_b-x_a)+y_ax_c-x_ay_c}.$$

求出$\beta$和$\gamma$后，我们就可以方便地在三角形内进行插值。从上面的讨论可以发现，$\alpha$、$\beta$、$\gamma$分别表示$P$点到$A$、$B$、$C$的接近程度，且$\alpha+\beta+\gamma=1$。对于某个依附于顶点的量$m$，我们可以用下式表示这个量在三角形内的插值结果：

$$m=\alpha m_a+\beta m_b+\gamma m_c.$$

重心坐标的值还有一个意义，具体见下图。

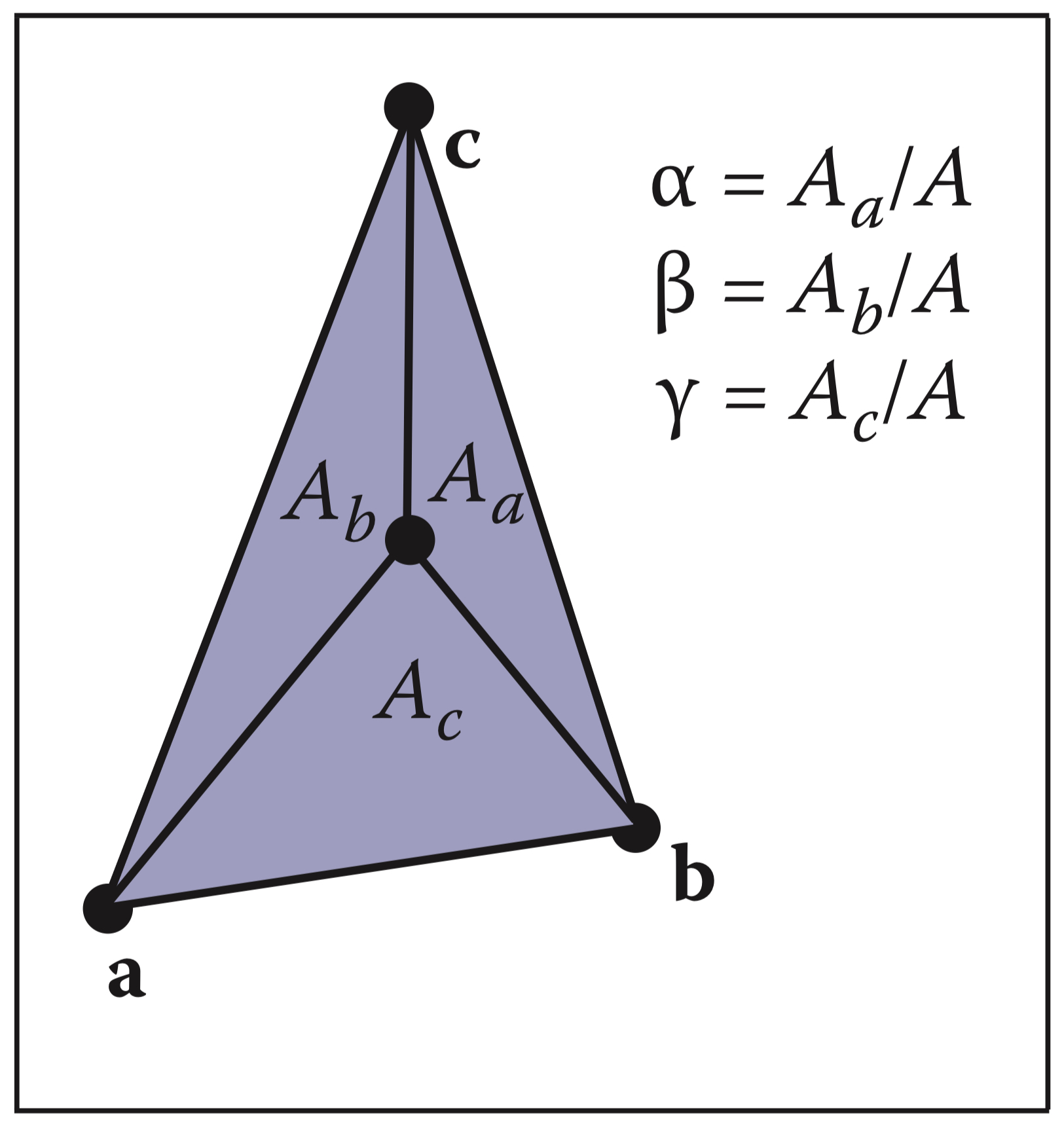
立体三角形

重心坐标可以被几乎无感地扩展到立体情况。仍延续上节对$\mathbf a$、$\mathbf b$、$\mathbf c$的定义，三角形的面积

$$S=\frac{1}{2}\left\|(\mathbf b-\mathbf a)\times(\mathbf c-\mathbf a)\right\|.$$

注意这里是不分正负的。三角形的法向量也很容易求出来：

$$\mathbf n=(\mathbf b-\mathbf a)\times(\mathbf c-\mathbf a),$$

其定向由$\vec{AB}$、$\vec{AC}$由右手定则确定。

参考重心坐标关于三角形面积的意义，我们可以得到立体三角形重心坐标的计算方法：

$$\alpha=\frac{\mathbf n\cdot\mathbf n_a}{\left\|\mathbf n\right\|^2},\\ \beta=\frac{\mathbf n\cdot\mathbf n_b}{\left\|\mathbf n\right\|^2},\\ \gamma=\frac{\mathbf n\cdot\mathbf n_c}{\left\|\mathbf n\right\|^2}.$$

其中

$$\mathbf n_a=(\mathbf c-\mathbf b)\times(\mathbf p-\mathbf b),\\ \mathbf n_b=(\mathbf p-\mathbf a)\times(\mathbf c-\mathbf a),\\ \mathbf n_c=(\mathbf b-\mathbf a)\times(\mathbf p-\mathbf a).$$

这三个矢量的定义不是唯一的，满足定向即可。